第一宇宙速度，作为物理学和航天工程中的关键概念，对于理解物体如何在地球附近空间进行稳定运动具有重要意义。本文将从第一宇宙速度的定义、计算公式及其推导过程、影响因素及应用等多个方面进行详细介绍，旨在帮助读者深入理解这一基本概念。

第一宇宙速度的定义

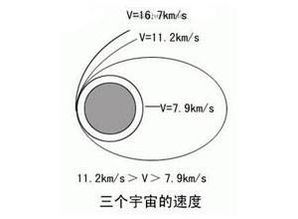
第一宇宙速度，通常被定义为物体绕地球表面作圆周运动所需的最小速度，也被称为环绕速度或航天器最小发射速度。在经典物理学中，其值被确定为7.9km/s。这一速度是实现地球轨道飞行的临界值，当物体达到或超过这一速度时，便能在地球引力作用下进行稳定的圆周运动而不至于掉落回地面。

计算公式及其推导过程

第一宇宙速度的计算公式为v1 = sqrt(GM/R)，其中G为万有引力常量，M为地球质量，R为地球半径。这一公式的推导过程基于万有引力定律和向心力原理。

万有引力定律

万有引力定律指出，两个物体之间的引力与它们质量的乘积成正比，与它们之间距离的平方成反比。其表达式为F = G * m1 * m2 / r^2。

向心力原理

当物体在圆周轨道上运动时，其向心力等于它所受的万有引力。向心力可以表示为F = m * v^2 / R。

公式推导

将万有引力定律和向心力原理的表达式相等，得到G * M * m / R^2 = m * v^2 / R。通过整理，可以得到v = sqrt(GM/R)。这就是第一宇宙速度的计算公式。

影响因素

尽管第一宇宙速度在经典物理学中被定义为7.9km/s，但其实际值会受到多种因素的影响。

地面位置的纬度

地球的自转会导致不同纬度地区的线速度有所不同。在赤道地区，由于自转速度最快，因此第一宇宙速度的实际值可能会略有增加。而在两极地区，由于自转速度几乎为零，第一宇宙速度则接近理论值7.9km/s。

海拔高度

随着海拔的增加，物体距离地球中心的距离也会增加。根据第一宇宙速度的计算公式，距离的增加会导致所需速度的降低。然而，这种影响在地球表面附近相对较小，只有在极高海拔或太空环境中才会变得显著。

自转速度

地球的自转不仅影响不同纬度地区的线速度，还会对航天器的发射和轨道设计产生影响。利用地球自转所带来的线速度，可以更加省力地发射航天器进入轨道。这种方法被称为“赤道飞行器发射”，在航天发射中得到了广泛应用。

应用

第一宇宙速度在航天工程和空间探索中具有重要应用。

航天器发射

为了实现地球轨道飞行，航天器必须达到或超过第一宇宙速度。在发射过程中，火箭需要提供足够的推力来克服地球引力并加速航天器达到所需的速度。一旦航天器进入轨道，它将在地球引力作用下以第一宇宙速度或更高的速度进行稳定的圆周运动。

卫星轨道设计

卫星的轨道设计需要考虑多种因素，包括轨道高度、轨道形状和轨道稳定性等。其中，第一宇宙速度是确定卫星能否维持稳定轨道的关键参数之一。通过精确计算和分析，可以设计出符合要求的卫星轨道，以确保卫星能够按照预定计划进行工作和数据传输。

深空探索

在深空探索中，第一宇宙速度也具有重要意义。虽然深空探测器不需要绕地球飞行，但在离开地球引力束缚进入宇宙空间的过程中，仍然需要达到一定的速度才能摆脱地球引力并实现稳定飞行。这一速度通常被称为第二宇宙速度或脱离速度。

注意事项

尽管第一宇宙速度在航天工程和空间探索中具有重要作用，但在实际应用中还需要注意以下几点：

1. 精确计算：在计算第一宇宙速度时，需要精确测量地球的质量和半径等参数，以确保结果的准确性。

2. 考虑影响因素：在实际应用中，需要考虑地面位置的纬度、海拔高度和自转速度等多种因素对第一宇宙速度的影响，以确保航天器的发射和轨道设计符合实际情况。

3. 安全措施：在航天发射和运行过程中，需要采取必要的安全措施来确保人员和设备的安全。例如，在发射过程中需要严格控制火箭的推力和飞行轨迹，以防止意外情况的发生。

总结

第一宇宙速度是物体绕地球表面作圆周运动所需的最小速度，其计算公式为v1 = sqrt(GM/R)。这一速度是实现地球轨道飞行的临界值，在航天工程和空间探索中具有重要作用。然而，其实际值会受到多种因素的影响，包括地面位置的纬度、海拔高度和自转速度等。因此，在实际应用中需要精确计算并考虑这些因素的影响，以确保航天器的发射和轨道设计符合实际情况。通过深入理解和应用第一宇宙速度的概念和计算公式，我们可以更好地开展航天工程和空间探索工作，为人类社会的科技进步和发展做出贡献。